Deterministic
chaos: a virtual experiment
Caos
deterministico: un esperimento virtuale
Download
serial version: main_serial.cpp
Download
parallel version: main_parallel_shared_memory.cpp
(parallelized with OpenMP)
ENGLISH:
This is a
C++ code which computes the basins of attraction of some attractors. The
attractors attract a particle following the classic Newton's law ma=F=Cm/r2
+ friction (C constant). The plan is discretized in a given number of points
and then the trajectory from each point is computed by an ODE solver (Euler I
order and Runge-Kutta IV order are implemented). Because of the friction, the
particle falls on one of the attractors, each of which is associated to a
color. Any initial point is then colored with the color of its attractor, thus
showing the basins of attraction of the attractors.
A large
number of parameters can be defined by the user as the number of pixels of the
final image, the ODE solver, the time step for the ODE solver, the number, the
position and the strength of attractors, the friction, and others.
ITALIAN:
Questo è un codice C++ che calcola il bacino di
attrazione di alcuni attrattori. Gli attrattori attraggono una particella con
la classica legge di Newton ma=F=Cm/r2 + attrito (C costante). Il
piano è discretizzato in un certo numero di punti e poi è calcolata la
traiettoria da ogni punto con un solutore di EDO (sono implementati Eulero I
ordine e Runge-Kutta IV ordine). A causa dell'attrito, la particella cade su
uno degli attrattori, ognuno dei quali è associato ad un colore. Ogni punto
iniziale è quindi colorato con il colore del suo attrattore, mostrando infine i
bacini di attrazione degli attrattori.
L'utente può scegliere il valore di molti parametri:
il numero di pixel dell'immagine finale, il solutore di ODE, il suo passo
temporale, il numero, la posizione e la forza degli attrattori, l'attrito, etc.
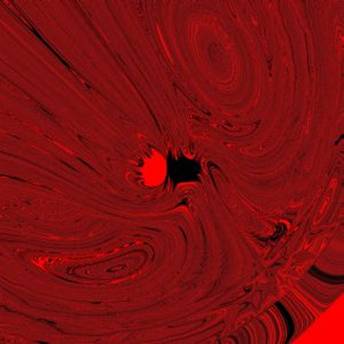
2 attractors, initial velocity = (0,0)